Groups.
Def. A set of elements with an operation is called a group if the following properties hold:
- Associativity :
- Identity : s.t.
- Inverse : s.t.
The group is called a commutative (Abelian) group if we have additionally
Example:
Fields.
Def. A set with 2 operations is called a field if the following properties hold:
- is a commutative group with identity element 0
- is also a commutative group with identity element 1
- Distributivity:
Example: For a consider such that , . Then is a field iff is prime.
Vector Spaces.
Def. Let be a field with identity elements 0 and 1. A vector space over the field is a set with a mapping and then:
- is a commutative group
- Multiplicative identity :
- Distributive property : and such that and
Function Spaces:
represents the space of all real valued functions on a set
Subspace.
Def. Let be a vector space, non-empty set, we call a subspace of if it is closed under linear combination:
Linear Combinations.
Def. vector space over , , then is called a Linear Combination. The set of all linear combinations of is called the span (linear hull) of .
The set is the generator of Span(). To find good generators, we need to know what is linear independence and dependence.
Linear Independence.
Def. A set of vectors is called linearly independent if
Basis.
Def. A subset of a vector space is called a (Hamel) basis if:
- is linearly independent
Proposition. If spans a vector space , then the set can be reduced to the basis of .
Proof.
- If is already linearly independent : Done
- If is dependent : there exists that is a linear combination of other vectors in , we remove it.
- We keep removing all until the remaining set is linearly independent
Def. A vector space is called finite dimensional if it contains a finite basis.
Prop. Let be a set of linearly independent vectors and be a finite dimensional vector space, then can be extended to a basis of .
Proof. (Sketch) Let be basis of . Consider the set . Remove vectors from the set until remaining vectors are linearly independent.
Corollary. Let be a finite dimensional vector space then any two basis of have the same length.
Dimension.
Def. The length of the basis of a finite dimensional vector space is called the dimension of .
Def. Assume that we have , subspaces of , the sum of the two spaces is defined as :
the sum is called the direct sum, if each element in the sum can be written in exactly one way.
This is a way of combining two (or more) subspaces into a larger vector space, in a way such that the decomposition of vectors is unique. For some vector space we can have have its unique constituents as follows:
Prop. Suppose is finite dimensional and is a subspace the there exists a subspace such that .
Proof. (Sketch) Let basis of extend it to a basis of , say the resulting set is
Define =
Linear Mapping.
Def. Let , vector space over , a mapping is called a linear if ,
the set of all linear mappings for is denoted . If then .
Def. then kernel (nullspace) of is defined as (all points that the transformation maps to 0).
Prop.
- is a subspace of U.
- is injective iff
Def. The range of is defined as .
Prop. The range is always a subspace of ( is surjective iff )
Def. For any set , the pre-image of is defined as
Prop. If is a subspace of , then is a subspace of
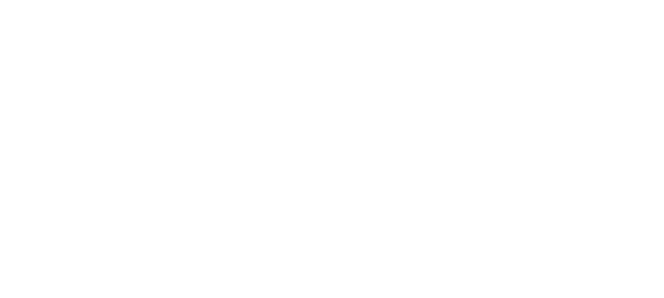
Theorem. Let be finite dimensional, any vector space, Let be a basis of Let be a basis of Then form a basis of In particular
Proof. Denote
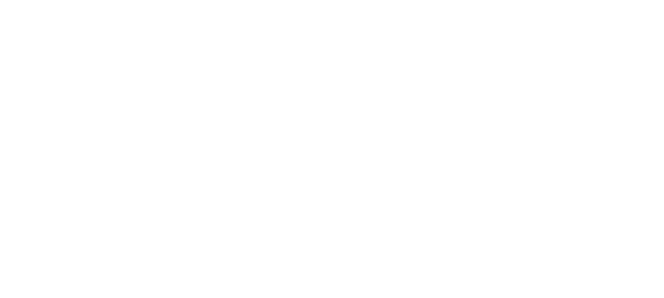 Step 1:
let , consider
s.t.
s.t.
Step 2: are linearly independent
Assume that
—(i)
only if since are bases.
Step 1:
let , consider
s.t.
s.t.
Step 2: are linearly independent
Assume that
—(i)
only if since are bases.
Prop. where , are finite dimensional. Then these following statements are equivalent
- is injective
- is surjective
- is bijective
Consider , are finite dimensional
Let, be a basis of be a basis of
-
-
Each image vector can be expressed in basis There exists coefficients such that
-
We may now stack these coefficients in a matrix:
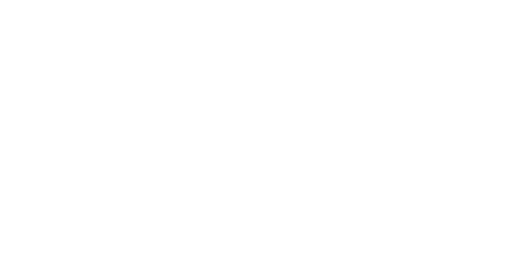 rows, one for each basis vector of
columns, one for each basis vector of
= matrix of mapping w.r.t. the basis of and of
rows, one for each basis vector of
columns, one for each basis vector of
= matrix of mapping w.r.t. the basis of and of
Notation: Let be linear, let be a basis of , basis of . We denote by the matrix corresponding to w.r.t bases and .
Properties of Matrices.
Let , vector spaces consider the basis fixed. Let
- For we have that
where is basis of .
- , linear, then